Introduction
Teachers are often faced with the dilemma of how to introduce a fresh concept in the classroom. This series aims at helping teachers create a structure that can help them put across concepts with clarity. Today’s topic is complex numbers and imaginary numbers.
Complex numbers & imaginary numbers are numbers that do not appear on the real number line. It is a concept that a lot of science students are faced with in their higher secondary education, but most of them get through those years without understanding the extraordinary scientific journey that led to its discovery and eventual application in the world of science and technology.
Types of Numbers
To understand what the term complex number means, it is important to know what the different classifications of numbers are. Numbers are classified into categories based on their utility to the mathematician, and they are as given below:
Natural Numbers
Natural numbers refer to the numbers that are used for counting and ordering in the real world. These are 1, 2, 3, and so on. These numbers are the first type of numbers that humans came across as a means of measuring the world around them and they continue to be so. For this reason, natural numbers are also known as counting numbers and are denoted by the letter N.
Whole Numbers
Even though there is no complete consensus on this, it is generally understood that whole numbers refer to the entire suite of counting numbers with the addition of zero to it at the beginning. The reason for this classification is because of calculus and its requirement in the process. The letter W is used to denote whole numbers.
Negative Numbers
Negative numbers refer to the numbers on the number line that lies to the left of zero. They can be essentially summed up as the additive inverse of the natural numbers. In simple terms, they are the numbers starting from -1, -2, -3, and so on.
Integers
An integer can be defined as a number that does not have a fractional component in it. So, essentially all the 3 types of numbers that are discussed above are integers. The natural numbers make up the positive integers and their additive inverse set represents negative integers. The letter Z is used to denote integers.
Rational Numbers
Rational numbers can be defined as the set of numbers that can be represented in the form of a p/q fraction that has a finite number of decimal places. For example, 1.5, -3.75, 9/44, and so on. The number can be rational even if the decimal places are never-ending, they just have to be recurring continuously, like in the case of ⅓, 1/9, and so on. The set of rational numbers includes natural numbers, integers, and those fractional components, and are referred to as Q.
Irrational Numbers
Irrational numbers are the set of numbers that cannot be represented by a p/q format and have a never-ending decimal expansion. Examples of such numbers include Euler’s constant e, pi, square root of rational numbers that are not squares of rational numbers themselves, and so on.
Real Numbers
The combined superset of rational and irrational numbers, which includes all the above-mentioned numbers on the number line represents the set of real numbers, which is represented by R.
Now that we know what real numbers are, it is time to shed light on what imaginary numbers are. However, there is a lot more to this than what meets the eye. The story of this particular type of number is very much real as opposed to its name. It all begins with the complicated relationship mathematics used to have with geometry, and a quest to find the solution to the cubic.
The Role of Geometry
Geometry is the study of the sizes, shapes, positions angles, and dimensions of things. Before the evolution of modern mathematics, geometry was the main source of truth. This was because mathematicians were used to dealing with real-world applications of mathematics, which is why most ancient civilizations like the Indians, Greeks, Babylonians, Egyptians, etc. all independently came up with their own versions of the Pythagoras Theorem, Euclidean Mathematics, algebra, etc. One such concept was the quadratic and cubic equations.
The solution to the quadratic equation has been known for several centuries. For any equation ax2 + bx + c = 0,

Where a, b, and c are real coefficients in the quadratic equation.
For example, in the equation
x2+26x = 27
Mathematicians found that the solution for this was the x = 1. However, for several centuries, mathematicians were completely oblivious to the negative solutions to the quadratic equation. In the case of the above equation, -27 is also a solution, but they were not aware of this. This was because of the way in which they used to solve the quadratic equation - using geometry. How, you might ask? Let us dive deeper into how they used to do it.
Solving the Quadratic with Geometry
Taking the above equation as a reference, ancient mathematicians would consider the x2 term as a literal square of side x, and the 26x term as a rectangle with one side 26 and the other side with length x. The areas of these two shapes needed to add up to 27.
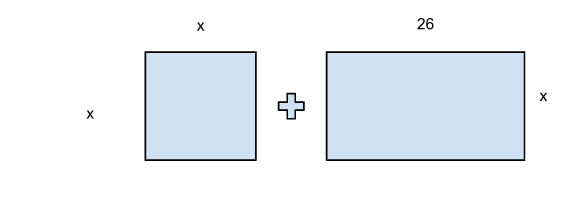
They cut the rectangle into equally shaped squares and rearranged them in the form of a square, with a few dimensions missing. Here the rectangle can be split in the form of squares with side 13. These missing dimensions could be figured out using the leftover part of the square, which in this case was a 13x13 square.
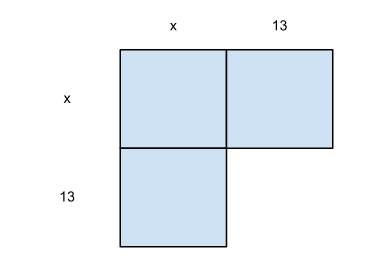
The square can be completed by adding the square of 13 (which represents the area it occupies) on both sides of the equation to maintain equality. So now the equation becomes (x+13)2 = 196. From here, the mathematicians could figure out that the square root of the equation was 14, which led to the answer 1.
The Problem
This was a great visual way of solving the quadratic equation, but this method posed a fundamental problem. X = -27 was willfully ignored as a solution to the equation because for them, it did not make sense - what real-world applications would a square of side -27 have? What did that even mean? So, in a way, they did not even acknowledge the existence of negative numbers - to the point where there was no single quadratic equation. They identified six different quadratic equations whose coefficients were positive and strictly stuck to those.
The Cubic
The same approach was used with the cubic equation ax3 + bx2 + cx + d = 0. However, this time, instead of using squares, they extended the idea of completing the square to add an extra dimension to account for the cube term, hence forming a cube. The first breakthrough in solving the cubic equation came from Scipione del Ferro, a mathematics professor at the University of Bologna. He used this method to find the solution to a subset of cubic equations called depressed cubics, a term used to refer to cubic equations without the x2 term. However, he did not publish his findings. It was rediscovered by his student Antonio Fior, who boasted of the same. He went on to challenge another mathematician Nicolo Fontana Tartaglia who eventually did find it using the same method. This sparked interest within the mathematics community, especially that of a polymath by the name of Gerolamo Cardano, who later learns the method from him. However, he took this one step further and found the solution to the full cubic equation including the x2 term. He did this by substituting the term x with (x-b/3a) where a and b are coefficients of the cubic equation and found that he could convert it into the form of a depressed cubic, which could then be solved using Tartaglia’s 3D-cube-slicing-and-rearranging technique. He published this in his book Ars Magna, which had a chapter about the solution to the cubic equation with geometric proof. However, this is where he encountered the problem that changed the way mathematicians viewed the subject - the square root of negative numbers.
The Breaking Point of Geometry
Cardano found that using his method in certain situations, he was getting the square roots of negative numbers as solutions to his equation. He walked back through the geometric proof of his method, which is where he found a geometric paradox.
For example, using the formula he could find that the area of a square was 30, and the sides were 5. So to complete the square, he had to somehow add an area of -5.
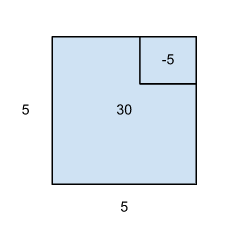
This is where the idea of imaginary numbers comes from, the idea of negative area. Cardano dismissed this problem, but later on, Rafael Bombelli, an Italian engineer, decided he wanted to find a solution. He allowed the square root of negative numbers to be their own new type of number, seeing that he couldn’t call it either positive or negative. He found that if he did this, he could eliminate the square root of the negative number, reaching a real answer. He called the intermediate number containing the real term and the term containing the square root of negative one a ‘complex number’, a term that stuck.
To understand this, let us take the example of the equation x3 + 2x2 = 3x + 10.
Here, one of the solutions to the cubic can be found using Cardano’s method, which is x = 2. However, when finding the other two roots, Bombelli runs into the same problem as Cardano, but by letting the answer be its own special type of number, he could find that the resulting root was 2-1. When he takes the final step and adds the numbers, the -1 term cancels out, leaving the answer as 4. This feels impossible because this proved that Cardano’s method did work, but the geometric proof that generated it had to be completely stepped over to reach that conclusion. This proved that negative areas must exist as an intermediate step on the way to the solution, even though the geometry didn’t make sense.
The Symbol i
This led to modern mathematics letting go of geometry as the ultimate form of truth. René Descartes (pronounced Re-nay-day-cart) named the square root of negative one as ‘imaginary numbers’ as a derogatory term, which stuck over the years. François Viète (pronounced frans-swa-vi-yet) created the modern symbolic notations used in mathematics today and later on, Euler used the letter i to denote the square root of negative one, which became its universal symbol.
Application of Imaginary Numbers
Armed with this notation, Euler derived Euler’s idenity, which is considered in the mathematics community as the most beautiful equation in mathematics, as it combined 5 constants (e, i, π, 1 and 0) and 3 mathematical operators (exponent, addition and multiplication) in one equation, all occurring only once. This equation is:
eiℼ + 1 = 0
Now comes the main question - if -1 did exist, if imaginary numbers and complex numbers did truly exist in the mathematical sense, did it have any practical application? Could i have any practical implications? This was finally answered by Erwin Schrödinger, an Austrian-Irish physicist. He found that the term eix perfectly describes the wave nature of particles. To understand why, we need to understand a very unique multiplicative property of imaginary numbers.
When a real number, let’s say 1, is multiplied by i, the product is an imaginary number. Multiply it ince more with i and the number becomes real again. If the number is 1, the resulting number would be negative one. Multiplying again, it becomes an imaginary number before becoming real again on further multiplication. So, it can be said that multiplying by i causes a number to dip in and out of the real and imaginary number lines, which are together known as the complex plane.
This is exactly how Schrödinger saw waves, as a combination of waves and particles, with the real part equivalent to a particle and the imaginary part equivalent to a wave. So when he formulated the Schrödinger wave equation, now one of the fundamental equations in quantum physics, imaginary numbers, and subsequently complex numbers, found their way into the heart of modern-day physics.
Conclusion
Science is an ever-evolving field, and new discoveries are being made all the time. One discovery might discredit the other, and it just reinforces the fickle nature of the universe. What René Descartes mockingly called an imaginary number found its way into an equation that described one of the most fundamental properties of the universe. In the words of physicist Freeman Dyson,
“.... the square root of minus one means that nature works with complex numbers and not just with real numbers…”
So imaginary numbers, recognized as the stopping point of mathematical reality, became the very basis of the way that we viewed reality. That is how science is and always will be, and that is why it is exciting to learn it.
Teachmint offers the best-in-class education ERP solutions to educational institutes. Do check it out to provide a hassle-free experience to your stakeholders and increase your student enrolment percentage. With our advanced learning management system, you can improve the teaching-learning experience.
Suggested Read: 4 Types of Evaluation Models to Assess Teachers












